So this question was asked to me in the first round of my interview with Google, and unfortunately I couldn’t crack it in the required time frame of 45 minutes. However, I pondered upon it and tried to solve it later and arrived at a solution that matched with the one stated in the problem statement. Bear with me for a while so that I can explain everything to you to the best of my capability :)
Problem statement
You are given a list of domain names (say www.example.com) and their corresponding scores (integer values). Your task is to find all the leaf domains, and the sum of their scores. Let me illustrate this with an example.
Suppose you have the following table of domains and their scores:
| Domain | Score |
|---|---|
com | 15 |
org | 20 |
test.com | 5 |
www.test.com | 10 |
mail.test.com | 25 |
test.abc.com | 60 |
www.test.abc.com | -20 |
Now going through the list of all these domains, you can observe that the domains www.test.com, mail.test.com, org and www.test.abc.com are not the part of any domain across the list, unlike test.com, which comes as a substring in www.test.com and mail.test.com. So, these domains are leaf domains and we need to calculate the sum of their scores. The important takeaway here is that we need to think like a domain resolver and organise the domains as they actually work in real life.
How do we calculate their scores? Let me illustrate with a nice little tree diagram:
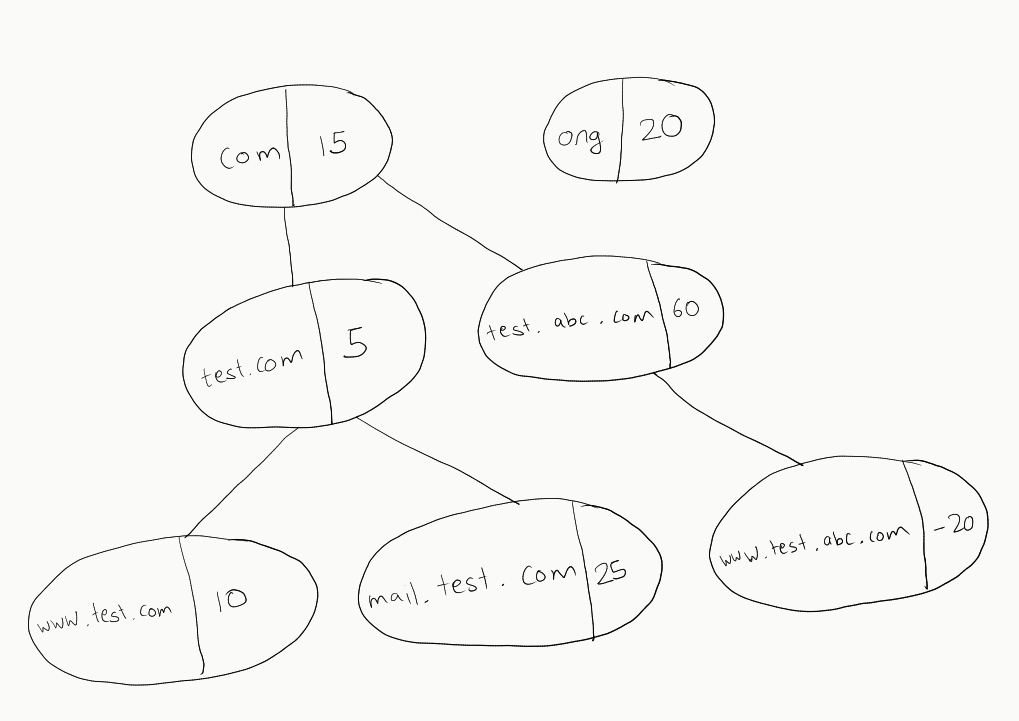
As you can see, this is how we can organise the domain names, with each string separated by . adds on to the tree level. This diagram also illustrates the leaf nodes perfectly.
Now to calculate leaf domain’s score, all we need to do is to calculate the root to leaf path sum for the leaf node in this domain tree. It can be illustrated as follows:
Suppose we need to calculate the score for www.test.com, so it can be done as:
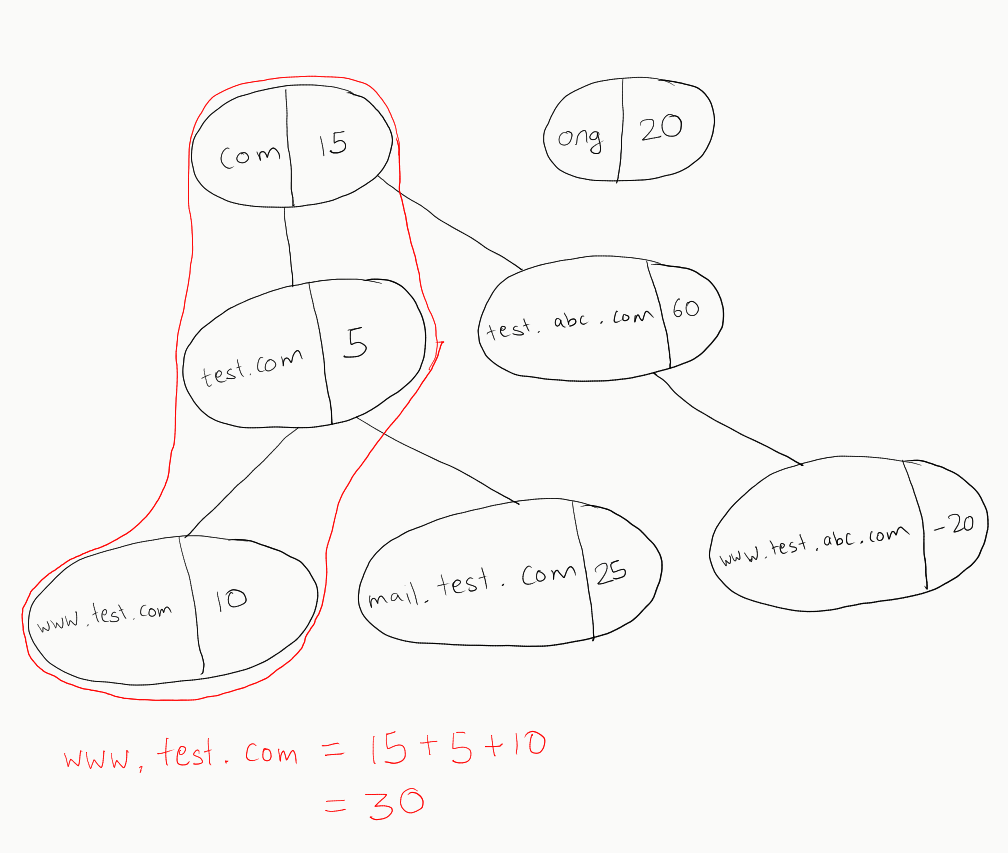
Now, we need to do this for each leaf node in the tree.
Constraints
- You can assume that the sum will always fit inside the normally available
Integerdatatype of any programming language - The domain name can be of any length, however for the context of this problem, no need of optimisation is needed for it
- Any node in the domain tree can have any number of children
- It is guaranteed that all the pairs of domain names and scores are unique, which means a specific domain cannot have multiple scores
Approach
- After going through the problem statement, it is clear that we need to calculate the root to leaf path sum of a tree in which each node can have
nchildren, which is a classic example of aTriedata structure. To help with the basics, the Wikipedia article on Trie as well as a sample problem on leetcode can help - We first need to build the Trie, by splitting each string by
.and forming a tree structure - Finally we’ll traverse the whole tree and calculate the root to leaf path sum for each leaf
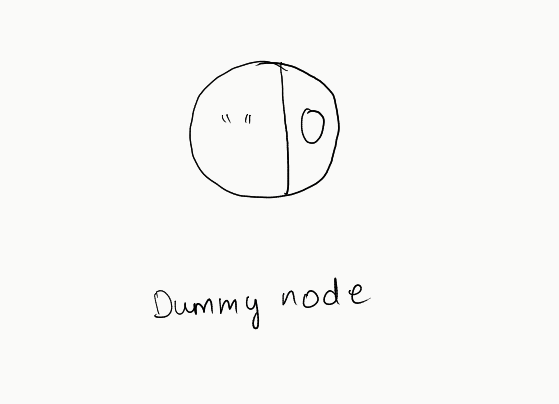
- In order to avoid a forest, we can create a dummy node and make the remaining nodes as its children, so that the top level domain doesn’t become a special case
Sample run
- Let’s say we want to insert the domains
www.test.abc.comandtest.abc.comin our trie structure - First of all we create a dummy node, with no keyword from domain and a score of 0
- Now, we take the domain
www.test.abc.com, split it into its keywords by., and reverse it. We are reversing it because the actual domain name system also works this way, wherecomis the top level domain, and then there are subdomains, that are present in the tree structure - Now we have the list of keywords to be inserted, which is
[com, abc, test, www]. We will insert those in order, like this:
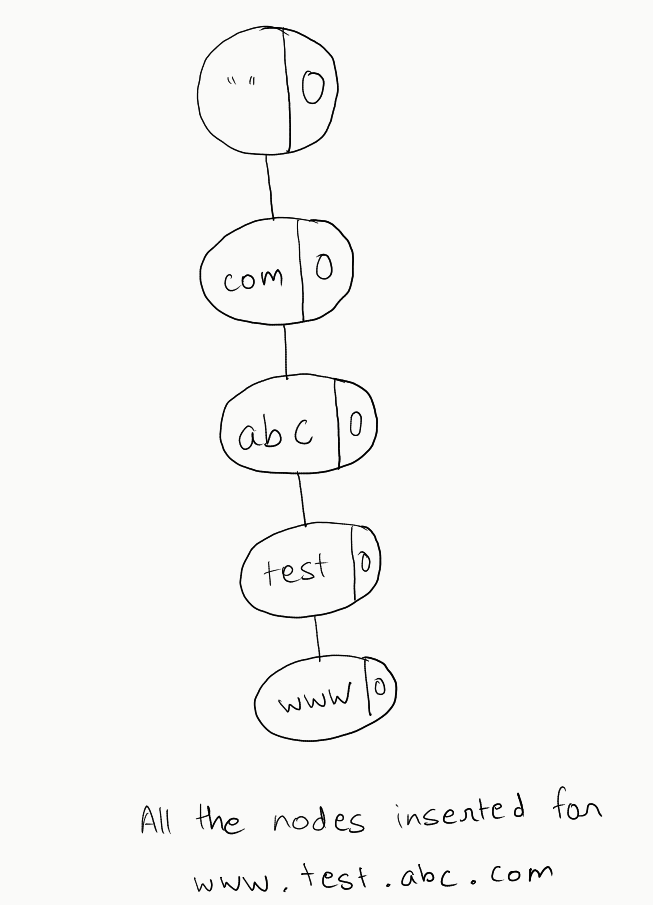
- Note that each node’s score is initially set to 0. This is because we don’t have the score of each individual keyword but for the whole domain. However, if we assign the score of the domain to the terminal keyword, our solution will still work as the other nodes don’t contribute to the sum. So we assign the score to
wwwhere as follows: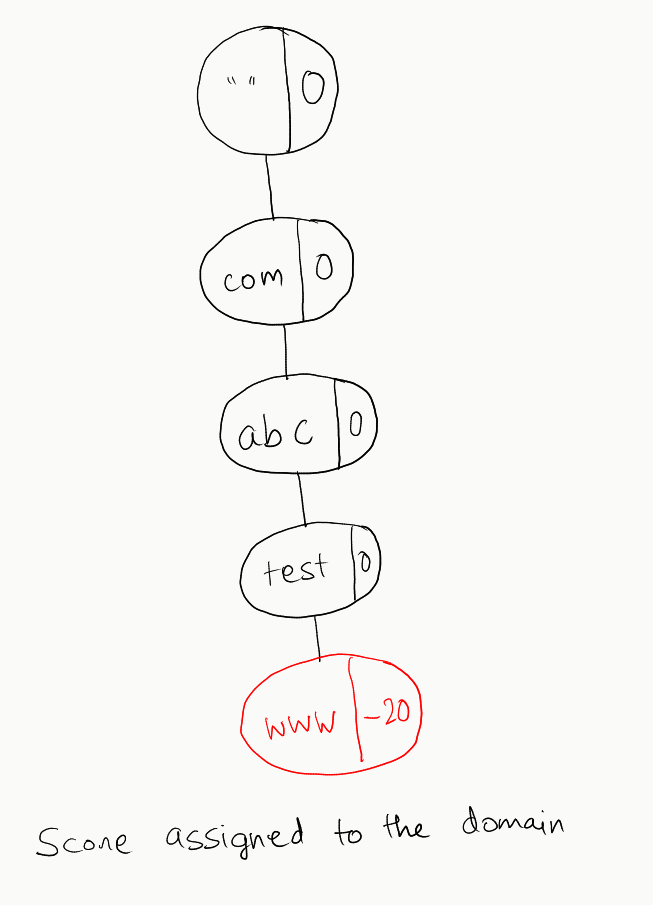
- Now we need to insert
test.abc.comin the tree, with the score of60. But if we look at the tree, the domaintest.abc.comis already present, and therefore we just need to assign the score to the terminal node for this domain, which istest. Hence, we can assign the score as follows: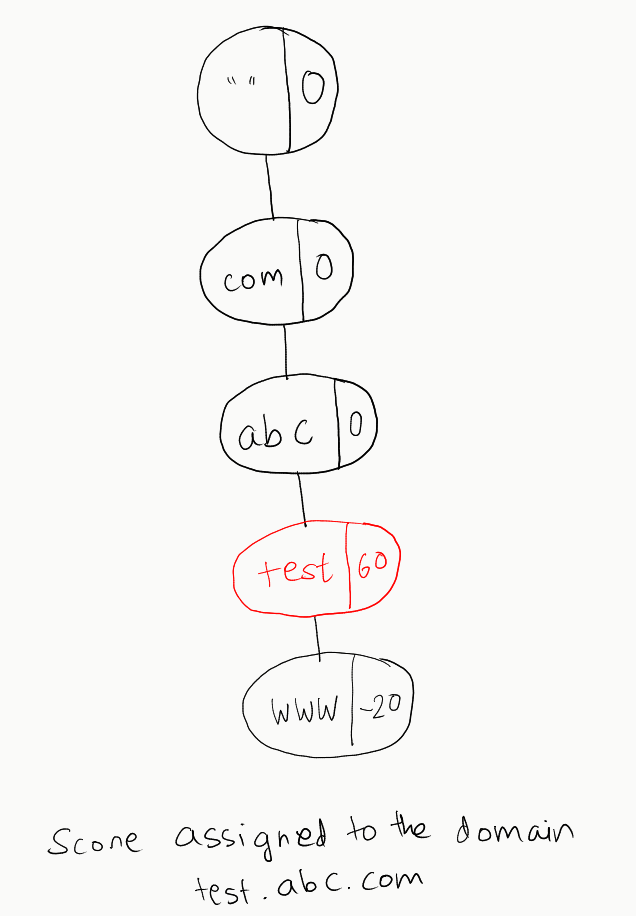
- In a similar fashion, we can insert all the given domains in our tree, and finally it would look like this:
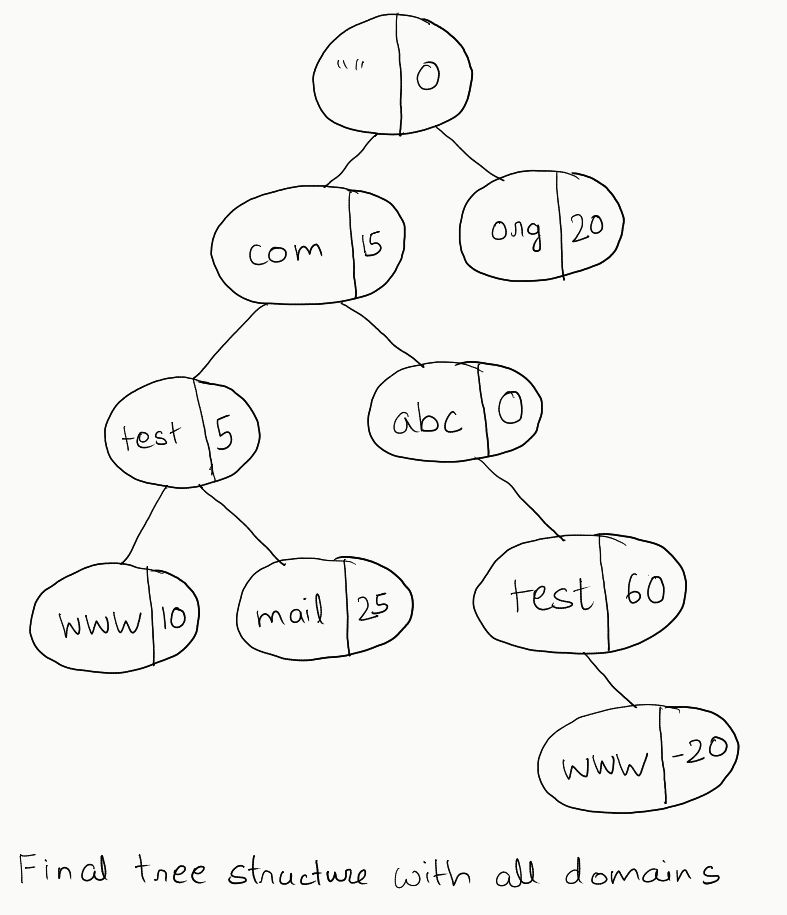
- Now, we can simply apply the root to leaf path sum on this tree using a backtracking algorithm, calculate the sum, and print the corresponding domain name.
Talk is cheap, show me the code
This is the C++ code for the logic explained above:
#include <bits/stdc++.h>
using namespace std;
/*
Auxillary method that will help us split the domain name string
based on the delimiter we provide
*/
vector<string> split(const string& str, char delimiter) {
vector<string> tokens;
int start = 0;
int end = str.find(delimiter);
while (end != std::string::npos) {
tokens.push_back(str.substr(start, end - start));
start = end + 1;
end = str.find(delimiter, start);
}
tokens.push_back(str.substr(start));
return tokens;
}
/**
* Auxilliary method that will help us join the domain name string using
* the delimiter we specify
*/
string join(vector<string>& list, char delimiter) {
stringstream res;
res << list[0];
for (int i = 1; i < list.size(); i++) {
res << delimiter;
res << list[i];
}
return res.str();
}
/**
* The node in our domain tree. Each node will have a keyword, a score
* and a map of its children.
*
* In the constructor, if the score is not supplied, then it is set to 0
* intentionally, as our root to leaf path sum will benefit from this property
*/
class TrieNode {
public:
string keyword;
int score;
unordered_map<string, TrieNode*> children;
TrieNode(string domain_name, int score) : keyword(domain_name), score(score) {}
TrieNode(string domain_name) : keyword(domain_name), score(0) {}
TrieNode() : keyword(""), score(0) {}
};
/**
* The tree class that will do all the heavy work for us
*/
class DomainTrie {
public:
TrieNode* root;
DomainTrie() {
this->root = new TrieNode();
}
void insert(string domain_name, int score) {
TrieNode* temp = this->root;
// split domain name by '.'
vector<string> words = split(domain_name, '.');
// reverse the domain name
reverse(words.begin(), words.end());
// for each word in the splitted domain name's list
for (string w : words) {
// check if the starting point's children contain the node.
// If no, then create a node and add it to the children's map
if (temp->children.find(w) == temp->children.end()) {
TrieNode* t = new TrieNode(w);
temp->children[w] = t;
}
// otherwise, just progress the pointer
temp = temp->children[w];
}
// set the score as well
temp->score = score;
}
};
void print_root_to_leaf_sum(TrieNode* root, vector<TrieNode*>& path) {
if (!root) return;
// if we don't see any children, then it is a leaf node
// and we calculate the sum as well as print it
if (root->children.size() == 0) {
int sum = 0;
vector<string> temp;
for (auto &node : path) {
sum += node->score;
temp.push_back(node->keyword);
}
reverse(temp.begin(), temp.end());
string domain_name = join(temp, '.');
cout << domain_name << ":\t" << sum << endl;
}
// otherwise recurse on the tree until you reach the leaf node
else {
for (auto entry : root->children) {
// push the node in path
path.push_back(entry.second);
// do the recursive call to calculate the sum
print_root_to_leaf_sum(entry.second, path);
// backtrack
path.pop_back();
}
}
}
int main() {
// Test run
DomainTrie* trie = new DomainTrie();
trie->insert("com", 15);
trie->insert("org", 20);
trie->insert("test.com", 5);
trie->insert("www.test.com", 10);
trie->insert("mail.test.com", 25);
trie->insert("www.test.abc.com", -20);
trie->insert("test.abc.com", 60);
vector<TrieNode*> path;
print_root_to_leaf_sum(trie->root, path);
return 0;
}- This code returns the following output, as expected:
org: 20
www.test.abc.com: 55
mail.test.com: 45
www.test.com: 30