Graph Binary Tree I

This question was asked to me in the first round of Google’s interview on 16th June 2025. I was able to solve it after an example given by the interviewer. Read along to know more :)

Problem statement

You are given an acyclic, undirected, connected graph in which each vertex has at most 3 neighbours. You have to find out whether the graph can also be a valid binary tree, and if yes, then return the integer id of vertex which can be used as the root of the tree. Otherwise, return -1.

For an example, consider the following graph:

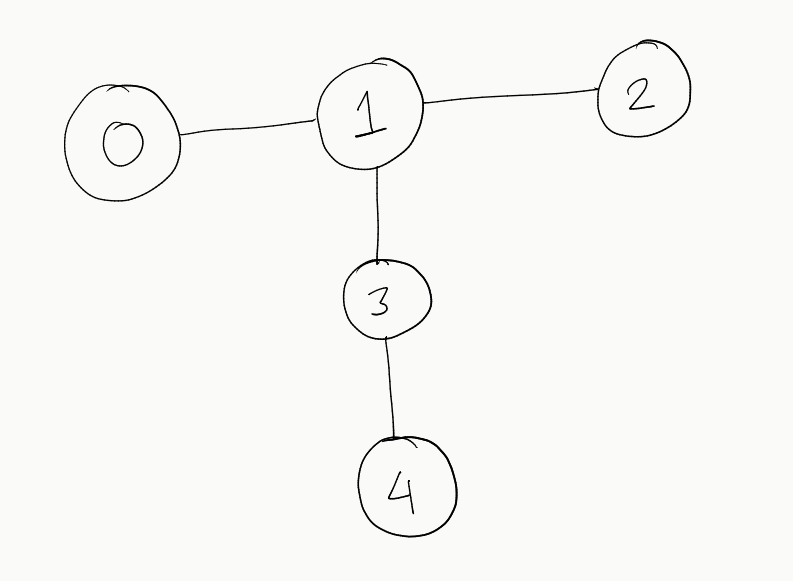
This could be represented in the form of an adjacency list as follows:

0 -> [1]
1 -> [0, 2, 3]
2 -> [1]
3 -> [1, 4]
4 -> [3]

Now, we need to find a vertex such that it can be considered as the root of the binary tree, if the graph can be represented as a tree.

Approach

If you think about it, half of the problem is already solved as mentioned in the problem statement. Well, in order for an undirected graph to be a valid tree, it has to satisfy two conditions:

1. The graph should not contain any cycle
2. The graph should be connected

More about this can be read here at GeeksForGeeks

In the problem statement, it is mentioned that the given graph is always acyclic and connected, so we are sure that the graph represents a valid tree. All we need to do now is to just find the root of that binary tree.

Intuition

Initially I wasn’t able to think of any solution, however, an example given by the interviewer made everything clear. Consider the graph that I represented earlier in the diagram:

Now, let’s try forming the tree from each node. I’ll just draw the graph in a tree-like format in order to make my point clear:

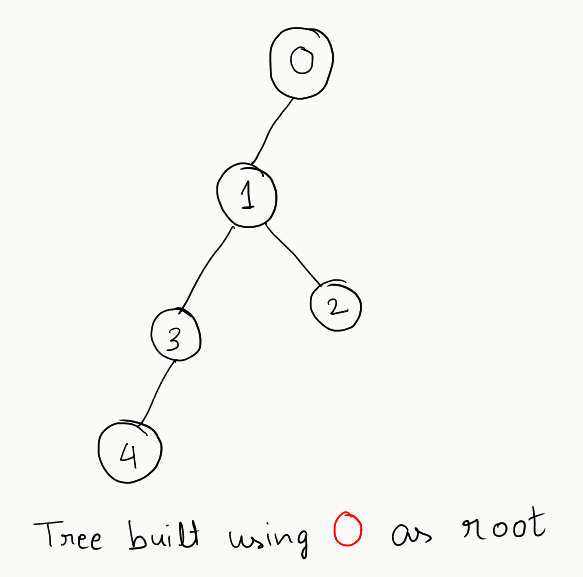
This is a valid binary tree. Let’s try with other nodes and see what results we get

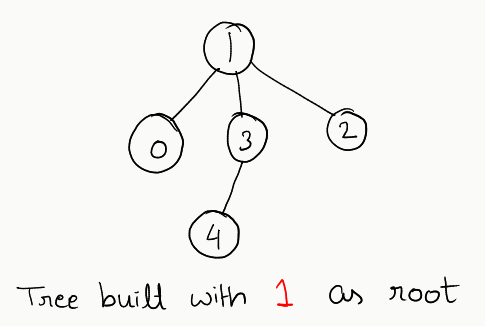
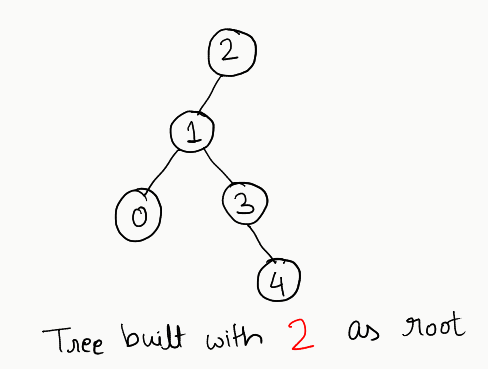
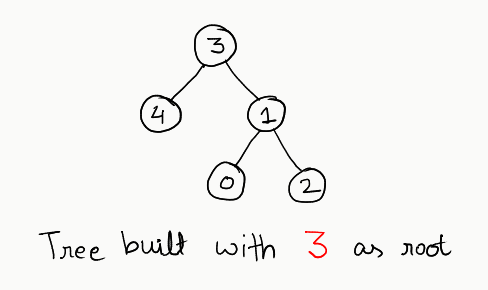
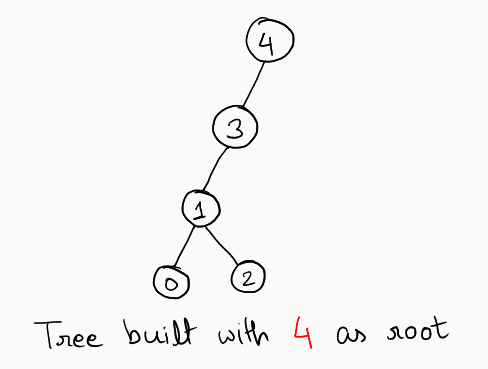
Consider all these trees, and you’ll find that in only one single case we don’t get a valid binary tree: when we build the tree using the vertex 1. In every other case, we get a valid tree.

So, what’s so special about the vertex 1? Well, considering its relationship carefully, it has 3 neighbours, and every other node has less than 3. So, essentially, the problem reduces to finding out which node has the number of neighbours less than 3. If we build the tree using any such node, we will end up having a valid binary tree.

Talk is cheap, show me the code

This is the C++ code for the logic explained above (The graph is represented as an adjacency list):

#include <bits/stdc++.h>
using namespace std;
int findRoot(vector<vector<int>>& adjacencyList) {
    int id = -1;
    for (int i = 0; i < adjacencyList.size(); i++) {
        if (adjacencyList[i].size() < 3) {
            id = i;
            break;
        }
    }
    return id;
}
 
int main() {
    vector<vector<int>> adjList = {
        {1},
        {0, 2, 3},
        {1},
        {1, 4},
        {3}
    };
    cout << findRoot(adjList);
    return 0;
}

This returns the following output:

0

Note that we had to return any of the vertex, so this is one of the possible answers. We could have returned 2, 3 or 4 as well.