Graph Binary Tree II

This question was asked to me in the first round of Google’s interview on 16th June 2025. I was able to solve it after an example given by the interviewer. This was the follow-up to the question Graph Binary Tree I, and if you haven’t gone through it, I’d highly recommend to check it out as it will be crucial for the understanding. Read along to know more :)

Problem statement

You are given an acyclic, undirected, connected graph in which each vertex has two properties, an integer id, and a colour, which can be either black or white, and has at most 3 neighbours. You have to find out whether the graph can also be a valid binary tree, and if yes, then return the integer id of vertex which can be used as the root of the tree. You also need to ensure that the colours of each level of the tree alternate, that is, your tree’s levels should look like either black->white->black->white or white->black->white->black.

The root vertex can be of any colour, however the rest of the levels should alternate between black and white.

If you cannot find any vertex that satisfies all these conditions, return -1.

Approach

At this point, if you’ve gone through Graph Binary Tree I, then you’ll be able to find the root. However, for the alternating colour constraint, we need to think more.

One possible approach that comes to mind, is by finding out all vertices that can be the candidate for our desired root, and then doing a BFS or level order traversal of the tree from every candidate vertex to check whether it satisfies the colour constraint or not. I had explained the same approach during my interview, however, the interviewer asked for a more optimal solution. Initially I couldn’t figure it out, but then he helped me with some examples that ultimately helped me solve it.

Intuition

Let’s try to re-use the example method which we did in Graph Binary Tree I, and try to find out the pattern.

Consider the following graph:

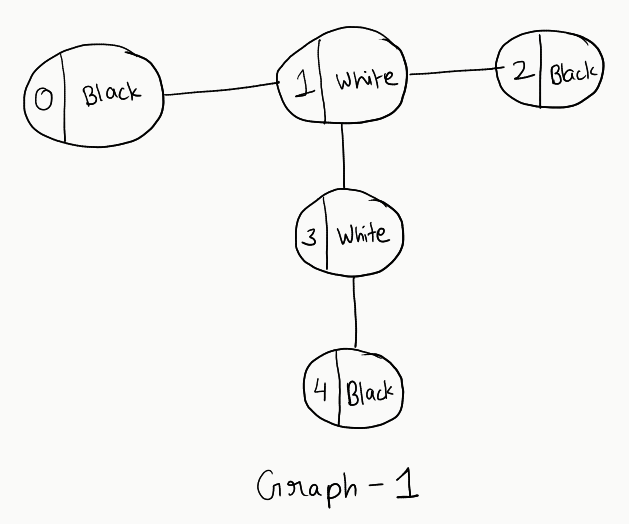
And let’s see all the tree formations according to our understanding developed earlier (Note that we are creating trees without considering the alternate colours on each level condition):

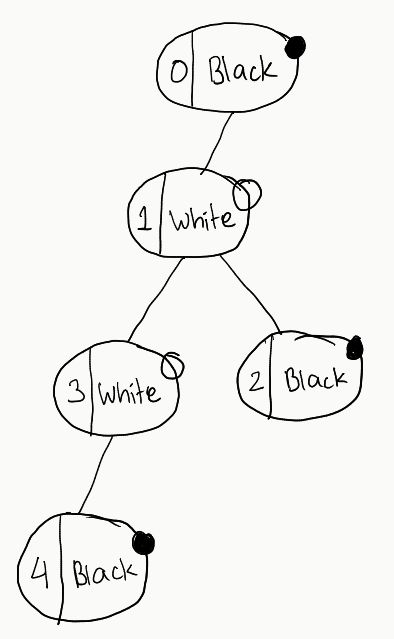
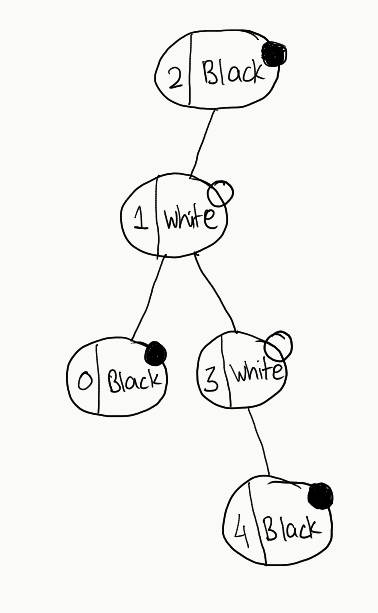
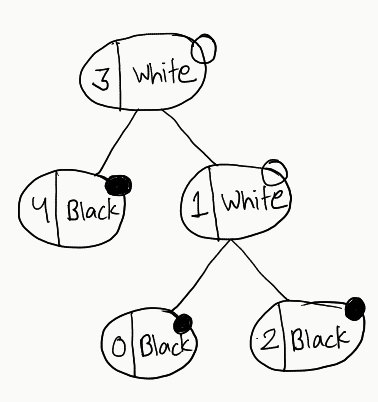
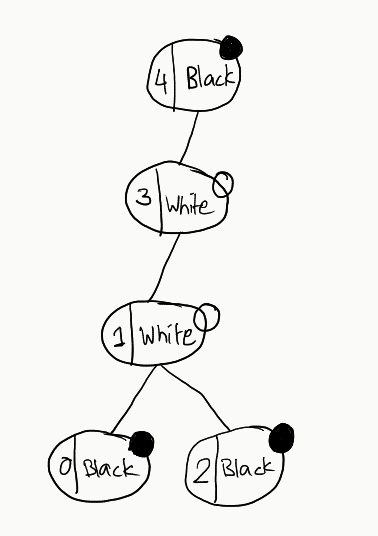
Go through all these trees. You’ll not find any single one that satisfies our condition. Now, let’s try out a different graph, with a slight modification in colours:

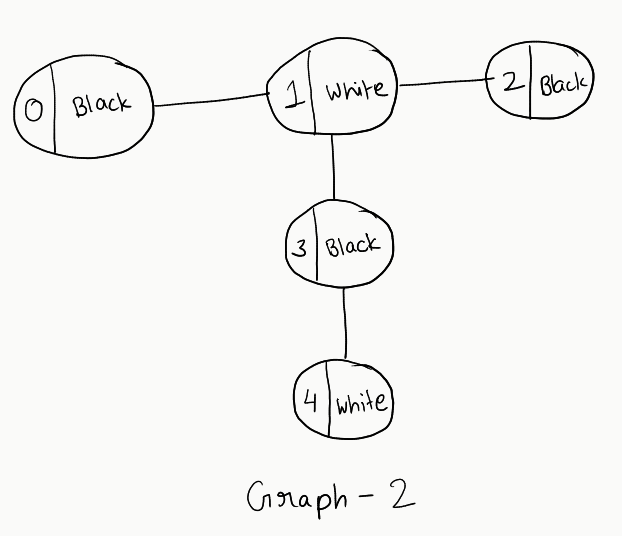
Let’s form the trees again, and see what difference we can observe

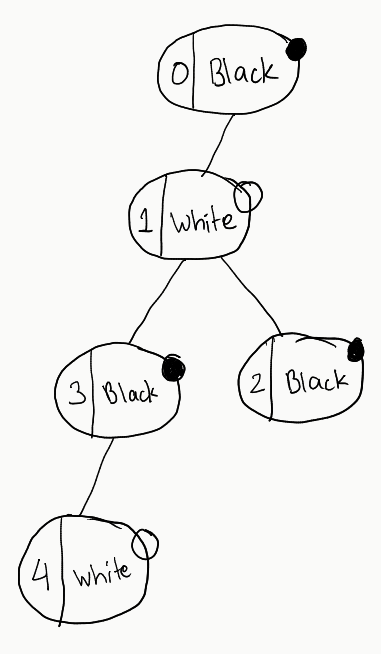
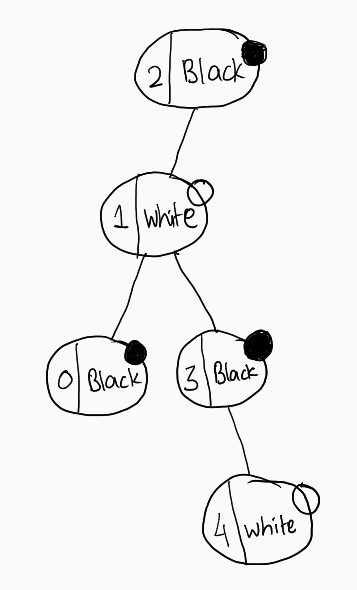
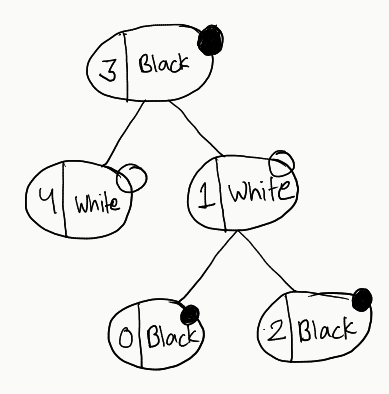
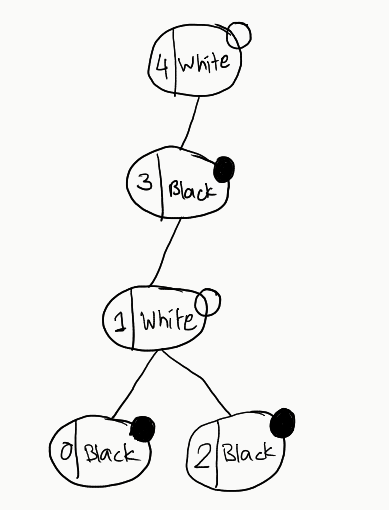
Now, observe all these trees. There is no tree that doesn’t satisfy our constraints. So, crux of the above exercise is: All we need to do is to just check for one tree. If it satisfies our constraints, we can go ahead and return it. If not, we just return -1 as there would no point in checking further.

Talk is cheap, show me the code

This is the C++ code for the logic explained above (The graph is represented here as an adjacency list):

#include <bits/stdc++.h>
using namespace std;
/*
In order to keep code simple, we are just using a color map
to store all the colors of nodes separately
*/
int findRoot(vector<vector<int>>& adjacencyList, unordered_map<int, string>& colorMap) {
    // We first find a required id
    int id = -1;
    for (int i = 0; i < adjacencyList.size(); i++) {
        if (adjacencyList[i].size() < 3) {
            id = i;
            break;
        }
    }
 
    // We then perform BFS traversal to check all the neighbours
    queue<int> q;
    q.push(id);
    set<int> visited;
    while (!q.empty())
    {
        int temp = q.front();
        q.pop();
        string color = colorMap[temp];
        visited.insert(temp);
        for (int i = 0; i < adjacencyList[temp].size(); i++) {
            int neighbor = adjacencyList[temp][i];
            if (colorMap[neighbor] != color) {
                // if the color alternates, then we should proceed
                if (visited.find(neighbor) == visited.end()) q.push(neighbor);
            } else {
                // we should return -1 directly
                return -1;
            }
        }
    }
 
    // if the BFS traversal succeeds, we can return the chosen id
    return id;
}
 
int main() {
    vector<vector<int>> adjList = {
        {1},
        {0, 2, 3},
        {1},
        {1, 4},
        {3}
    };
 
    unordered_map<int, string> colorMap1;
    colorMap1[0] = "black";
    colorMap1[1] = "white";
    colorMap1[2] = "black";
    colorMap1[3] = "white";
    colorMap1[4] = "black";
 
    unordered_map<int, string> colorMap2;
    colorMap2[0] = "black";
    colorMap2[1] = "white";
    colorMap2[2] = "black";
    colorMap2[3] = "black";
    colorMap2[4] = "white";
 
    cout << findRoot(adjList, colorMap1) << "\n";
    cout << findRoot(adjList, colorMap2) << "\n";
    return 0;
}

This returns the following output:

-1
0

which is in accordance with both the examples illustrated. Thanks for reading :)